Introduction to Python#
Getting Started#
To run the labs in this book, you will need two things:
An installation of
Python3, which is the specific version ofPythonused in the labs.Access to
Jupyter, a very popularPythoninterface that runs code through a file called a notebook.
You can download and install Python3 by following the instructions available at anaconda.com.
There are a number of ways to get access to Jupyter. Here are just a few:
Using Google’s
Colaboratoryservice: colab.research.google.com/.Using
JupyterHub, available at jupyter.org/hub.Using your own
jupyterinstallation. Installation instructions are available at jupyter.org/install.
Please see the Python resources page on the book website statlearning.com for up-to-date information about getting Python and Jupyter working on your computer.
You will need to install the ISLP package, which provides access to the datasets and custom-built functions that we provide.
Inside a macOS or Linux terminal type pip install ISLP; this also installs most other packages needed in the labs. The Python resources page has a link to the ISLP documentation website.
To run this lab, download the file Ch2-statlearn-lab.ipynb from the Python resources page.
Now run the following code at the command line: jupyter lab Ch2-statlearn-lab.ipynb.
If you’re using Windows, you can use the start menu to access anaconda, and follow the links. For example, to install ISLP and run this lab, you can run the same code above in an anaconda shell.
Basic Commands#
In this lab, we will introduce some simple Python commands.
For more resources about Python in general, readers may want to consult the tutorial at docs.python.org/3/tutorial/.
Like most programming languages, Python uses functions
to perform operations. To run a
function called fun, we type
fun(input1,input2), where the inputs (or arguments)
input1 and input2 tell
Python how to run the function. A function can have any number of
inputs. For example, the
print() function outputs a text representation of all of its arguments to the console.
print('fit a model with', 11, 'variables')
fit a model with 11 variables
The following command will provide information about the print() function.
print?
Adding two integers in Python is pretty intuitive.
3 + 5
8
In Python, textual data is handled using
strings. For instance, "hello" and
'hello'
are strings.
We can concatenate them using the addition + symbol.
"hello" + " " + "world"
'hello world'
A string is actually a type of sequence: this is a generic term for an ordered list.
The three most important types of sequences are lists, tuples, and strings.
We introduce lists now.
The following command instructs Python to join together
the numbers 3, 4, and 5, and to save them as a
list named x. When we
type x, it gives us back the list.
x = [3, 4, 5]
x
[3, 4, 5]
Note that we used the brackets
[] to construct this list.
We will often want to add two sets of numbers together. It is reasonable to try the following code, though it will not produce the desired results.
y = [4, 9, 7]
x + y
[3, 4, 5, 4, 9, 7]
The result may appear slightly counterintuitive: why did Python not add the entries of the lists
element-by-element?
In Python, lists hold arbitrary objects, and are added using concatenation.
In fact, concatenation is the behavior that we saw earlier when we entered "hello" + " " + "world".
This example reflects the fact that
Python is a general-purpose programming language. Much of Python’s data-specific
functionality comes from other packages, notably numpy
and pandas.
In the next section, we will introduce the numpy package.
See docs.scipy.org/doc/numpy/user/quickstart.html for more information about numpy.
Introduction to Numerical Python#
As mentioned earlier, this book makes use of functionality that is contained in the numpy
library, or package. A package is a collection of modules that are not necessarily included in
the base Python distribution. The name numpy is an abbreviation for numerical Python.
To access numpy, we must first import it.
import numpy as np
In the previous line, we named the numpy module np; an abbreviation for easier referencing.
In numpy, an array is a generic term for a multidimensional
set of numbers.
We use the np.array() function to define x and y, which are one-dimensional arrays, i.e. vectors.
x = np.array([3, 4, 5])
y = np.array([4, 9, 7])
Note that if you forgot to run the import numpy as np command earlier, then
you will encounter an error in calling the np.array() function in the previous line.
The syntax np.array() indicates that the function being called
is part of the numpy package, which we have abbreviated as np.
Since x and y have been defined using np.array(), we get a sensible result when we add them together. Compare this to our results in the previous section,
when we tried to add two lists without using numpy.
x + y
array([ 7, 13, 12])
In numpy, matrices are typically represented as two-dimensional arrays, and vectors as one-dimensional arrays. {While it is also possible to create matrices using np.matrix(), we will use np.array() throughout the labs in this book.}
We can create a two-dimensional array as follows.
x = np.array([[1, 2], [3, 4]])
x
array([[1, 2],
[3, 4]])
The object x has several
attributes, or associated objects. To access an attribute of x, we type x.attribute, where we replace attribute
with the name of the attribute.
For instance, we can access the ndim attribute of x as follows.
x.ndim
2
The output indicates that x is a two-dimensional array.
Similarly, x.dtype is the data type attribute of the object x. This indicates that x is
comprised of 64-bit integers:
x.dtype
dtype('int64')
Why is x comprised of integers? This is because we created x by passing in exclusively integers to the np.array() function.
If
we had passed in any decimals, then we would have obtained an array of
floating point numbers (i.e. real-valued numbers).
np.array([[1, 2], [3.0, 4]]).dtype
dtype('float64')
Typing fun? will cause Python to display
documentation associated with the function fun, if it exists.
We can try this for np.array().
np.array?
This documentation indicates that we could create a floating point array by passing a dtype argument into np.array().
np.array([[1, 2], [3, 4]], float).dtype
dtype('float64')
The array x is two-dimensional. We can find out the number of rows and columns by looking
at its shape attribute.
x.shape
(2, 2)
A method is a function that is associated with an
object.
For instance, given an array x, the expression
x.sum() sums all of its elements, using the sum()
method for arrays.
The call x.sum() automatically provides x as the
first argument to its sum() method.
x = np.array([1, 2, 3, 4])
x.sum()
10
We could also sum the elements of x by passing in x as an argument to the np.sum() function.
x = np.array([1, 2, 3, 4])
np.sum(x)
10
As another example, the
reshape() method returns a new array with the same elements as
x, but a different shape.
We do this by passing in a tuple in our call to
reshape(), in this case (2, 3). This tuple specifies that we would like to create a two-dimensional array with
\(2\) rows and \(3\) columns. {Like lists, tuples represent a sequence of objects. Why do we need more than one way to create a sequence? There are a few differences between tuples and lists, but perhaps the most important is that elements of a tuple cannot be modified, whereas elements of a list can be.}
In what follows, the
\n character creates a new line.
x = np.array([1, 2, 3, 4, 5, 6])
print('beginning x:\n', x)
x_reshape = x.reshape((2, 3))
print('reshaped x:\n', x_reshape)
beginning x:
[1 2 3 4 5 6]
reshaped x:
[[1 2 3]
[4 5 6]]
The previous output reveals that numpy arrays are specified as a sequence
of rows. This is called row-major ordering, as opposed to column-major ordering.
Python (and hence numpy) uses 0-based
indexing. This means that to access the top left element of x_reshape,
we type in x_reshape[0,0].
x_reshape[0, 0]
1
Similarly, x_reshape[1,2] yields the element in the second row and the third column
of x_reshape.
x_reshape[1, 2]
6
Similarly, x[2] yields the
third entry of x.
Now, let’s modify the top left element of x_reshape. To our surprise, we discover that the first element of x has been modified as well!
print('x before we modify x_reshape:\n', x)
print('x_reshape before we modify x_reshape:\n', x_reshape)
x_reshape[0, 0] = 5
print('x_reshape after we modify its top left element:\n', x_reshape)
print('x after we modify top left element of x_reshape:\n', x)
x before we modify x_reshape:
[1 2 3 4 5 6]
x_reshape before we modify x_reshape:
[[1 2 3]
[4 5 6]]
x_reshape after we modify its top left element:
[[5 2 3]
[4 5 6]]
x after we modify top left element of x_reshape:
[5 2 3 4 5 6]
Modifying x_reshape also modified x because the two objects occupy the same space in memory.
We just saw that we can modify an element of an array. Can we also modify a tuple? It turns out that we cannot — and trying to do so introduces an exception, or error.
my_tuple = (3, 4, 5)
my_tuple[0] = 2
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[23], line 2
1 my_tuple = (3, 4, 5)
----> 2 my_tuple[0] = 2
TypeError: 'tuple' object does not support item assignment
We now briefly mention some attributes of arrays that will come in handy. An array’s shape attribute contains its dimension; this is always a tuple.
The ndim attribute yields the number of dimensions, and T provides its transpose.
x_reshape.shape, x_reshape.ndim, x_reshape.T
((2, 3),
2,
array([[5, 4],
[2, 5],
[3, 6]]))
Notice that the three individual outputs (2,3), 2, and array([[5, 4],[2, 5], [3,6]]) are themselves output as a tuple.
We will often want to apply functions to arrays.
For instance, we can compute the
square root of the entries using the np.sqrt() function:
np.sqrt(x)
array([2.23606798, 1.41421356, 1.73205081, 2. , 2.23606798,
2.44948974])
We can also square the elements:
x**2
array([25, 4, 9, 16, 25, 36])
We can compute the square roots using the same notation, raising to the power of \(1/2\) instead of 2.
x**0.5
array([2.23606798, 1.41421356, 1.73205081, 2. , 2.23606798,
2.44948974])
Throughout this book, we will often want to generate random data.
The np.random.normal() function generates a vector of random
normal variables. We can learn more about this function by looking at the help page, via a call to np.random.normal?.
The first line of the help page reads normal(loc=0.0, scale=1.0, size=None).
This signature line tells us that the function’s arguments are loc, scale, and size. These are keyword arguments, which means that when they are passed into
the function, they can be referred to by name (in any order). {Python also uses positional arguments. Positional arguments do not need to use a keyword. To see an example, type in np.sum?. We see that a is a positional argument, i.e. this function assumes that the first unnamed argument that it receives is the array to be summed. By contrast, axis and dtype are keyword arguments: the position in which these arguments are entered into np.sum() does not matter.}
By default, this function will generate random normal variable(s) with mean (loc) \(0\) and standard deviation (scale) \(1\); furthermore,
a single random variable will be generated unless the argument to size is changed.
We now generate 50 independent random variables from a \(N(0,1)\) distribution.
x = np.random.normal(size=50)
x
array([-0.03210033, 2.88589878, 2.032346 , -0.97740449, 0.74976584,
0.01587522, 0.35190955, 0.38563727, 0.68222768, -2.79167026,
0.5315963 , -2.12373777, 0.45925793, 0.68404957, 1.41798295,
0.82797542, -1.67717772, -0.30470384, -3.01527216, -1.19004471,
0.32159721, 0.86196753, 1.68960457, 0.11442239, -1.19875984,
1.47416641, 0.28691704, 0.31760358, -0.30078932, -0.05081133,
1.36044547, -0.58373321, 0.97960509, 0.11763553, 0.5407772 ,
0.14147888, 0.39073386, -0.70075092, -0.81496835, -0.29053756,
1.12035224, -1.67577201, 0.63278064, 0.35813289, -0.95009155,
-0.52783458, 1.1152048 , 0.2889721 , 1.3899747 , -0.35350308])
We create an array y by adding an independent \(N(50,1)\) random variable to each element of x.
y = x + np.random.normal(loc=50, scale=1, size=50)
The np.corrcoef() function computes the correlation matrix between x and y. The off-diagonal elements give the
correlation between x and y.
np.corrcoef(x, y)
array([[1. , 0.80944295],
[0.80944295, 1. ]])
If you’re following along in your own Jupyter notebook, then you probably noticed that you got a different set of results when you ran the past few
commands. In particular,
each
time we call np.random.normal(), we will get a different answer, as shown in the following example.
print(np.random.normal(scale=5, size=2))
print(np.random.normal(scale=5, size=2))
[ 1.19248357 -3.34094548]
[0.41370731 0.21864656]
In order to ensure that our code provides exactly the same results
each time it is run, we can set a random seed
using the
np.random.default_rng() function.
This function takes an arbitrary, user-specified integer argument. If we set a random seed before
generating random data, then re-running our code will yield the same results. The
object rng has essentially all the random number generating methods found in np.random. Hence, to
generate normal data we use rng.normal().
rng = np.random.default_rng(1303)
print(rng.normal(scale=5, size=2))
rng2 = np.random.default_rng(1303)
print(rng2.normal(scale=5, size=2))
[ 4.09482632 -1.07485605]
[ 4.09482632 -1.07485605]
Throughout the labs in this book, we use np.random.default_rng() whenever we
perform calculations involving random quantities within numpy. In principle, this
should enable the reader to exactly reproduce the stated results. However, as new versions of numpy become available, it is possible
that some small discrepancies may occur between the output
in the labs and the output
from numpy.
The np.mean(), np.var(), and np.std() functions can be used
to compute the mean, variance, and standard deviation of arrays. These functions are also
available as methods on the arrays.
rng = np.random.default_rng(3)
y = rng.standard_normal(10)
np.mean(y), y.mean()
(-0.1126795190952861, -0.1126795190952861)
np.var(y), y.var(), np.mean((y - y.mean())**2)
(2.7243406406465125, 2.7243406406465125, 2.7243406406465125)
Notice that by default np.var() divides by the sample size \(n\) rather
than \(n-1\); see the ddof argument in np.var?.
np.sqrt(np.var(y)), np.std(y)
(1.6505576756498128, 1.6505576756498128)
The np.mean(), np.var(), and np.std() functions can also be applied to the rows and columns of a matrix.
To see this, we construct a \(10 \times 3\) matrix of \(N(0,1)\) random variables, and consider computing its row sums.
X = rng.standard_normal((10, 3))
X
array([[ 0.22578661, -0.35263079, -0.28128742],
[-0.66804635, -1.05515055, -0.39080098],
[ 0.48194539, -0.23855361, 0.9577587 ],
[-0.19980213, 0.02425957, 1.54582085],
[ 0.54510552, -0.50522874, -0.18283897],
[ 0.54052513, 1.93508803, -0.26962033],
[-0.24355868, 1.0023136 , -0.88645994],
[-0.29172023, 0.88253897, 0.58035002],
[ 0.0915167 , 0.67010435, -2.82816231],
[ 1.02130682, -0.95964476, -1.66861984]])
Since arrays are row-major ordered, the first axis, i.e. axis=0, refers to its rows. We pass this argument into the mean() method for the object X.
X.mean(axis=0)
array([ 0.15030588, 0.14030961, -0.34238602])
The following yields the same result.
X.mean(0)
array([ 0.15030588, 0.14030961, -0.34238602])
Graphics#
In Python, common practice is to use the library
matplotlib for graphics.
However, since Python was not written with data analysis in mind,
the notion of plotting is not intrinsic to the language.
We will use the subplots() function
from matplotlib.pyplot to create a figure and the
axes onto which we plot our data.
For many more examples of how to make plots in Python,
readers are encouraged to visit matplotlib.org/stable/gallery/.
In matplotlib, a plot consists of a figure and one or more axes. You can think of the figure as the blank canvas upon which
one or more plots will be displayed: it is the entire plotting window.
The axes contain important information about each plot, such as its \(x\)- and \(y\)-axis labels,
title, and more. (Note that in matplotlib, the word axes is not the plural of axis: a plot’s axes contains much more information
than just the \(x\)-axis and the \(y\)-axis.)
We begin by importing the subplots() function
from matplotlib. We use this function
throughout when creating figures.
The function returns a tuple of length two: a figure
object as well as the relevant axes object. We will typically
pass figsize as a keyword argument.
Having created our axes, we attempt our first plot using its plot() method.
To learn more about it,
type ax.plot?.
from matplotlib.pyplot import subplots
fig, ax = subplots(figsize=(8, 8))
x = rng.standard_normal(100)
y = rng.standard_normal(100)
ax.plot(x, y);
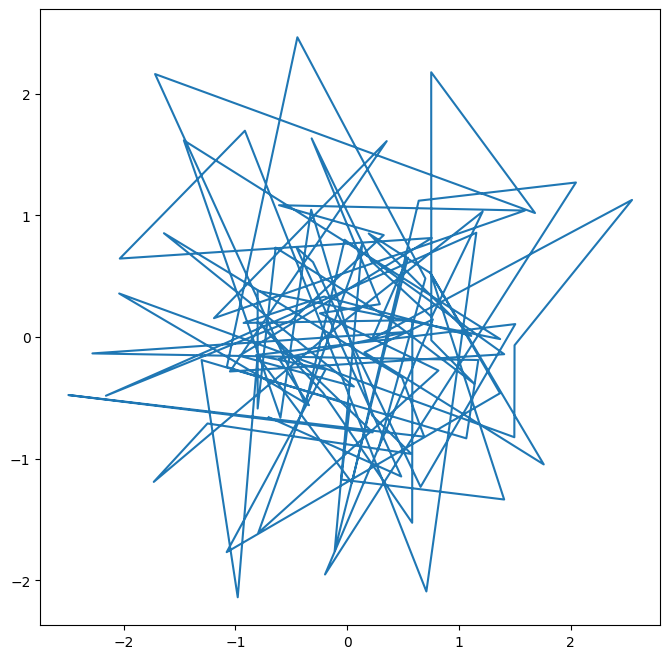
We pause here to note that we have unpacked the tuple of length two returned by subplots() into the two distinct
variables fig and ax. Unpacking
is typically preferred to the following equivalent but slightly more verbose code:
output = subplots(figsize=(8, 8))
fig = output[0]
ax = output[1]
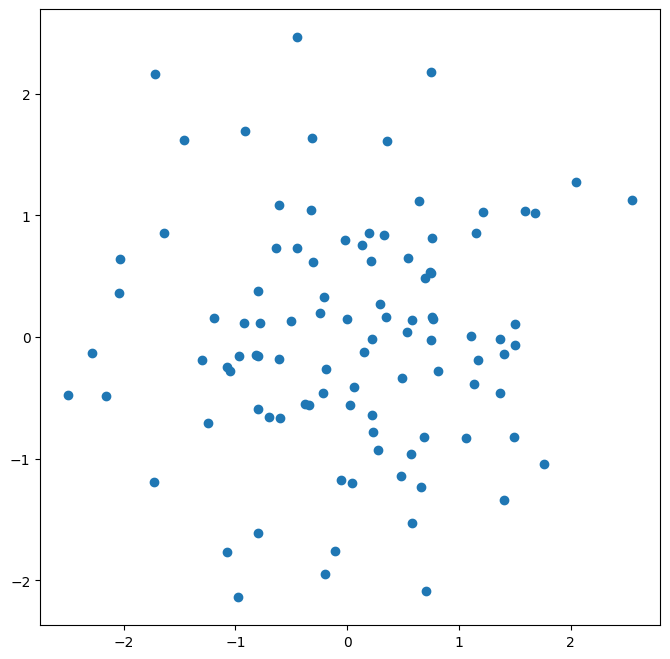
We see that our earlier cell produced a line plot, which is the default. To create a scatterplot, we provide an additional argument to ax.plot(), indicating that circles should be displayed.
fig, ax = subplots(figsize=(8, 8))
ax.plot(x, y, 'o');
Different values of this additional argument can be used to produce different colored lines as well as different linestyles.
As an alternative, we could use the ax.scatter() function to create a scatterplot.
fig, ax = subplots(figsize=(8, 8))
ax.scatter(x, y, marker='o');

Notice that in the code blocks above, we have ended
the last line with a semicolon. This prevents ax.plot(x, y) from printing
text to the notebook. However, it does not prevent a plot from being produced.
If we omit the trailing semi-colon, then we obtain the following output:
fig, ax = subplots(figsize=(8, 8))
ax.scatter(x, y, marker='o')
<matplotlib.collections.PathCollection at 0x7f4521d622d0>

In what follows, we will use trailing semicolons whenever the text that would be output is not germane to the discussion at hand.
To label our plot, we make use of the set_xlabel(), set_ylabel(), and set_title() methods
of ax.
fig, ax = subplots(figsize=(8, 8))
ax.scatter(x, y, marker='o')
ax.set_xlabel("this is the x-axis")
ax.set_ylabel("this is the y-axis")
ax.set_title("Plot of X vs Y");
Having access to the figure object fig itself means that we can go in and change some aspects and then redisplay it. Here, we change
the size from (8, 8) to (12, 3).
fig.set_size_inches(12,3)
fig
Occasionally we will want to create several plots within a figure. This can be
achieved by passing additional arguments to subplots().
Below, we create a \(2 \times 3\) grid of plots
in a figure of size determined by the figsize argument. In such
situations, there is often a relationship between the axes in the plots. For example,
all plots may have a common \(x\)-axis. The subplots() function can automatically handle
this situation when passed the keyword argument sharex=True.
The axes object below is an array pointing to different plots in the figure.
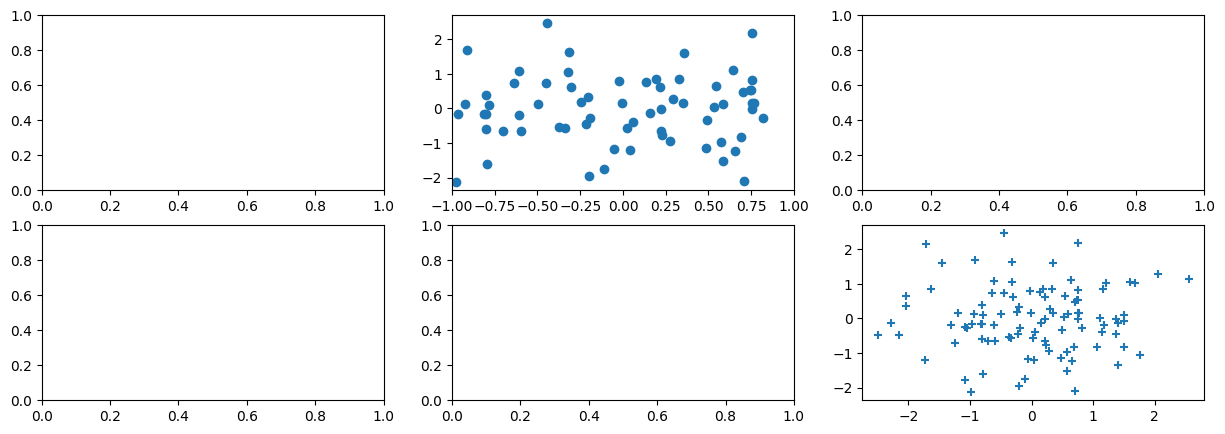
fig, axes = subplots(nrows=2,
ncols=3,
figsize=(15, 5))
We now produce a scatter plot with 'o' in the second column of the first row and
a scatter plot with '+' in the third column of the second row.
axes[0,1].plot(x, y, 'o')
axes[1,2].scatter(x, y, marker='+')
fig
Type subplots? to learn more about
subplots().
To save the output of fig, we call its savefig()
method. The argument dpi is the dots per inch, used
to determine how large the figure will be in pixels.
fig.savefig("Figure.png", dpi=400)
fig.savefig("Figure.pdf", dpi=200);
We can continue to modify fig using step-by-step updates; for example, we can modify the range of the \(x\)-axis, re-save the figure, and even re-display it.
axes[0,1].set_xlim([-1,1])
fig.savefig("Figure_updated.jpg")
fig
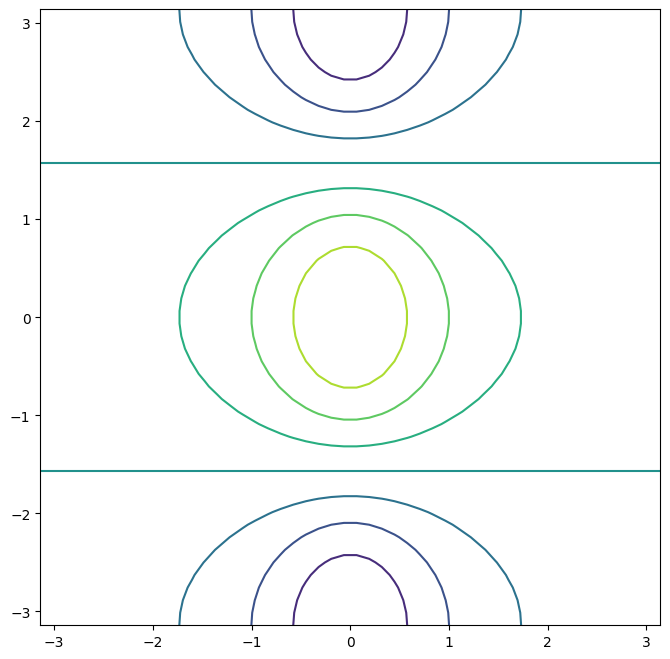
We now create some more sophisticated plots. The
ax.contour() method produces a contour plot
in order to represent three-dimensional data, similar to a
topographical map. It takes three arguments:
A vector of
xvalues (the first dimension),A vector of
yvalues (the second dimension), andA matrix whose elements correspond to the
zvalue (the third dimension) for each pair of(x,y)coordinates.
To create x and y, we’ll use the command np.linspace(a, b, n),
which returns a vector of n numbers starting at a and ending at b.
fig, ax = subplots(figsize=(8, 8))
x = np.linspace(-np.pi, np.pi, 50)
y = x
f = np.multiply.outer(np.cos(y), 1 / (1 + x**2))
ax.contour(x, y, f);
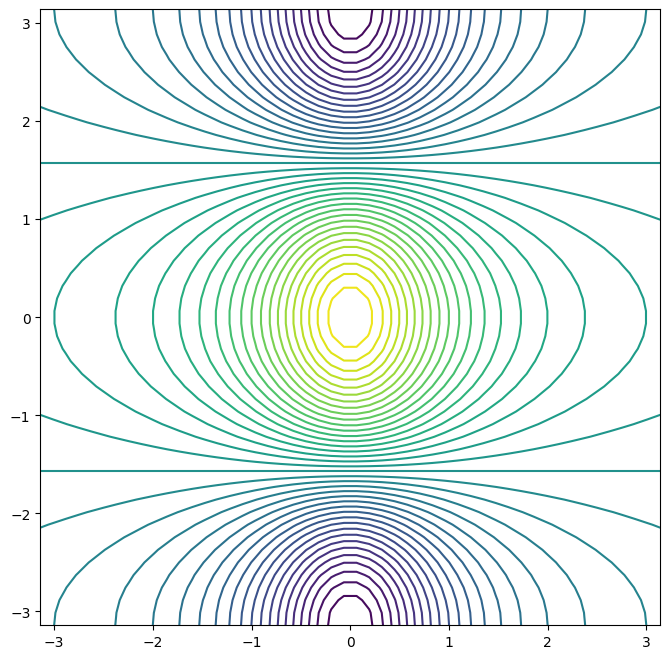
We can increase the resolution by adding more levels to the image.
fig, ax = subplots(figsize=(8, 8))
ax.contour(x, y, f, levels=45);
To fine-tune the output of the
ax.contour() function, take a
look at the help file by typing ?plt.contour.
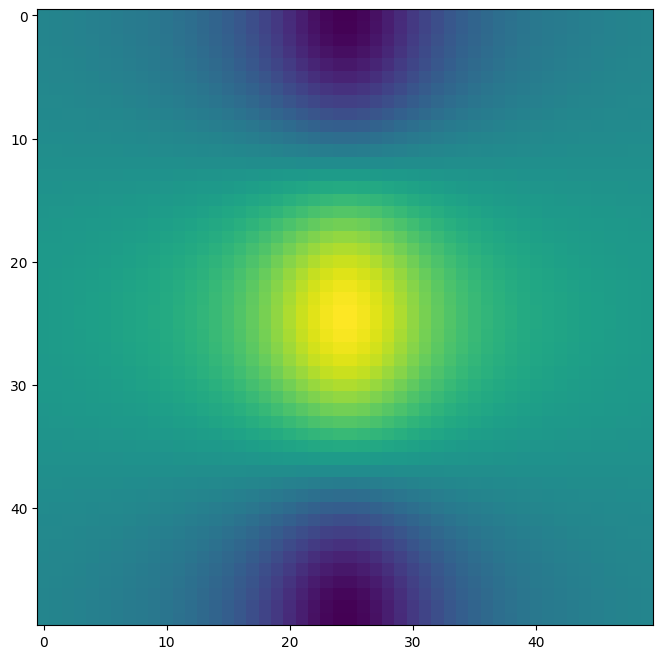
The ax.imshow() method is similar to
ax.contour(), except that it produces a color-coded plot
whose colors depend on the z value. This is known as a
heatmap, and is sometimes used to plot temperature in
weather forecasts.
fig, ax = subplots(figsize=(8, 8))
ax.imshow(f);
Sequences and Slice Notation#
As seen above, the
function np.linspace() can be used to create a sequence
of numbers.
seq1 = np.linspace(0, 10, 11)
seq1
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
The function np.arange()
returns a sequence of numbers spaced out by step. If step is not specified, then a default value of \(1\) is used. Let’s create a sequence
that starts at \(0\) and ends at \(10\).
seq2 = np.arange(0, 10)
seq2
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
Why isn’t \(10\) output above? This has to do with slice notation in Python.
Slice notation
is used to index sequences such as lists, tuples and arrays.
Suppose we want to retrieve the fourth through sixth (inclusive) entries
of a string. We obtain a slice of the string using the indexing notation [3:6].
"hello world"[3:6]
'lo '
In the code block above, the notation 3:6 is shorthand for slice(3,6) when used inside
[].
"hello world"[slice(3,6)]
'lo '
You might have expected slice(3,6) to output the fourth through seventh characters in the text string (recalling that Python begins its indexing at zero), but instead it output the fourth through sixth.
This also explains why the earlier np.arange(0, 10) command output only the integers from \(0\) to \(9\).
See the documentation slice? for useful options in creating slices.
Indexing Data#
To begin, we create a two-dimensional numpy array.
A = np.array(np.arange(16)).reshape((4, 4))
A
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
Typing A[1,2] retrieves the element corresponding to the second row and third
column. (As usual, Python indexes from \(0.\))
A[1,2]
6
The first number after the open-bracket symbol [
refers to the row, and the second number refers to the column.
Indexing Rows, Columns, and Submatrices#
To select multiple rows at a time, we can pass in a list
specifying our selection. For instance, [1,3] will retrieve the second and fourth rows:
A[[1,3]]
array([[ 4, 5, 6, 7],
[12, 13, 14, 15]])
To select the first and third columns, we pass in [0,2] as the second argument in the square brackets.
In this case we need to supply the first argument :
which selects all rows.
A[:,[0,2]]
array([[ 0, 2],
[ 4, 6],
[ 8, 10],
[12, 14]])
Now, suppose that we want to select the submatrix made up of the second and fourth rows as well as the first and third columns. This is where indexing gets slightly tricky. It is natural to try to use lists to retrieve the rows and columns:
A[[1,3],[0,2]]
array([ 4, 14])
Oops — what happened? We got a one-dimensional array of length two identical to
np.array([A[1,0],A[3,2]])
array([ 4, 14])
Similarly, the following code fails to extract the submatrix comprised of the second and fourth rows and the first, third, and fourth columns:
A[[1,3],[0,2,3]]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[63], line 1
----> 1 A[[1,3],[0,2,3]]
IndexError: shape mismatch: indexing arrays could not be broadcast together with shapes (2,) (3,)
We can see what has gone wrong here. When supplied with two indexing lists, the numpy interpretation is that these provide pairs of \(i,j\) indices for a series of entries. That is why the pair of lists must have the same length. However, that was not our intent, since we are looking for a submatrix.
One easy way to do this is as follows. We first create a submatrix by subsetting the rows of A, and then on the fly we make a further submatrix by subsetting its columns.
A[[1,3]][:,[0,2]]
array([[ 4, 6],
[12, 14]])
There are more efficient ways of achieving the same result.
The convenience function np.ix_() allows us to extract a submatrix
using lists, by creating an intermediate mesh object.
idx = np.ix_([1,3],[0,2,3])
A[idx]
array([[ 4, 6, 7],
[12, 14, 15]])
Alternatively, we can subset matrices efficiently using slices.
The slice
1:4:2 captures the second and fourth items of a sequence, while the slice 0:3:2 captures
the first and third items (the third element in a slice sequence is the step size).
A[1:4:2,0:3:2]
array([[ 4, 6],
[12, 14]])
Why are we able to retrieve a submatrix directly using slices but not using lists?
Its because they are different Python types, and
are treated differently by numpy.
Slices can be used to extract objects from arbitrary sequences, such as strings, lists, and tuples, while the use of lists for indexing is more limited.
Boolean Indexing#
In numpy, a Boolean is a type that equals either True or False (also represented as \(1\) and \(0\), respectively).
The next line creates a vector of \(0\)’s, represented as Booleans, of length equal to the first dimension of A.
keep_rows = np.zeros(A.shape[0], bool)
keep_rows
array([False, False, False, False])
We now set two of the elements to True.
keep_rows[[1,3]] = True
keep_rows
array([False, True, False, True])
Note that the elements of keep_rows, when viewed as integers, are the same as the
values of np.array([0,1,0,1]). Below, we use == to verify their equality. When
applied to two arrays, the == operation is applied elementwise.
np.all(keep_rows == np.array([0,1,0,1]))
True
(Here, the function np.all() has checked whether
all entries of an array are True. A similar function, np.any(), can be used to check whether any entries of an array are True.)
However, even though np.array([0,1,0,1]) and keep_rows are equal according to ==, they index different sets of rows!
The former retrieves the first, second, first, and second rows of A.
A[np.array([0,1,0,1])]
array([[0, 1, 2, 3],
[4, 5, 6, 7],
[0, 1, 2, 3],
[4, 5, 6, 7]])
By contrast, keep_rows retrieves only the second and fourth rows of A — i.e. the rows for which the Boolean equals TRUE.
A[keep_rows]
array([[ 4, 5, 6, 7],
[12, 13, 14, 15]])
This example shows that Booleans and integers are treated differently by numpy.
We again make use of the np.ix_() function
to create a mesh containing the second and fourth rows, and the first, third, and fourth columns. This time, we apply the function to Booleans,
rather than lists.
keep_cols = np.zeros(A.shape[1], bool)
keep_cols[[0, 2, 3]] = True
idx_bool = np.ix_(keep_rows, keep_cols)
A[idx_bool]
array([[ 4, 6, 7],
[12, 14, 15]])
We can also mix a list with an array of Booleans in the arguments to np.ix_():
idx_mixed = np.ix_([1,3], keep_cols)
A[idx_mixed]
array([[ 4, 6, 7],
[12, 14, 15]])
For more details on indexing in numpy, readers are referred
to the numpy tutorial mentioned earlier.
Loading Data#
Data sets often contain different types of data, and may have names associated with the rows or columns.
For these reasons, they typically are best accommodated using a
data frame.
We can think of a data frame as a sequence
of arrays of identical length; these are the columns. Entries in the
different arrays can be combined to form a row.
The pandas
library can be used to create and work with data frame objects.
Reading in a Data Set#
The first step of most analyses involves importing a data set into
Python.
Before attempting to load
a data set, we must make sure that Python knows where to find the file containing it.
If the
file is in the same location
as this notebook file, then we are all set.
Otherwise,
the command
os.chdir() can be used to change directory. (You will need to call import os before calling os.chdir().)
We will begin by reading in Auto.csv, available on the book website. This is a comma-separated file, and can be read in using pd.read_csv():
import pandas as pd
Auto = pd.read_csv('Auto.csv')
Auto
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | name | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 18.0 | 8 | 307.0 | 130 | 3504 | 12.0 | 70 | 1 | chevrolet chevelle malibu |
| 1 | 15.0 | 8 | 350.0 | 165 | 3693 | 11.5 | 70 | 1 | buick skylark 320 |
| 2 | 18.0 | 8 | 318.0 | 150 | 3436 | 11.0 | 70 | 1 | plymouth satellite |
| 3 | 16.0 | 8 | 304.0 | 150 | 3433 | 12.0 | 70 | 1 | amc rebel sst |
| 4 | 17.0 | 8 | 302.0 | 140 | 3449 | 10.5 | 70 | 1 | ford torino |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 387 | 27.0 | 4 | 140.0 | 86 | 2790 | 15.6 | 82 | 1 | ford mustang gl |
| 388 | 44.0 | 4 | 97.0 | 52 | 2130 | 24.6 | 82 | 2 | vw pickup |
| 389 | 32.0 | 4 | 135.0 | 84 | 2295 | 11.6 | 82 | 1 | dodge rampage |
| 390 | 28.0 | 4 | 120.0 | 79 | 2625 | 18.6 | 82 | 1 | ford ranger |
| 391 | 31.0 | 4 | 119.0 | 82 | 2720 | 19.4 | 82 | 1 | chevy s-10 |
392 rows × 9 columns
The book website also has a whitespace-delimited version of this data, called Auto.data. This can be read in as follows:
Auto = pd.read_csv('Auto.data', delim_whitespace=True)
Both Auto.csv and Auto.data are simply text
files. Before loading data into Python, it is a good idea to view it using
a text editor or other software, such as Microsoft Excel.
We now take a look at the column of Auto corresponding to the variable horsepower:
Auto['horsepower']
0 130.0
1 165.0
2 150.0
3 150.0
4 140.0
...
392 86.00
393 52.00
394 84.00
395 79.00
396 82.00
Name: horsepower, Length: 397, dtype: object
We see that the dtype of this column is object.
It turns out that all values of the horsepower column were interpreted as strings when reading
in the data.
We can find out why by looking at the unique values.
np.unique(Auto['horsepower'])
array(['100.0', '102.0', '103.0', '105.0', '107.0', '108.0', '110.0',
'112.0', '113.0', '115.0', '116.0', '120.0', '122.0', '125.0',
'129.0', '130.0', '132.0', '133.0', '135.0', '137.0', '138.0',
'139.0', '140.0', '142.0', '145.0', '148.0', '149.0', '150.0',
'152.0', '153.0', '155.0', '158.0', '160.0', '165.0', '167.0',
'170.0', '175.0', '180.0', '190.0', '193.0', '198.0', '200.0',
'208.0', '210.0', '215.0', '220.0', '225.0', '230.0', '46.00',
'48.00', '49.00', '52.00', '53.00', '54.00', '58.00', '60.00',
'61.00', '62.00', '63.00', '64.00', '65.00', '66.00', '67.00',
'68.00', '69.00', '70.00', '71.00', '72.00', '74.00', '75.00',
'76.00', '77.00', '78.00', '79.00', '80.00', '81.00', '82.00',
'83.00', '84.00', '85.00', '86.00', '87.00', '88.00', '89.00',
'90.00', '91.00', '92.00', '93.00', '94.00', '95.00', '96.00',
'97.00', '98.00', '?'], dtype=object)
We see the culprit is the value ?, which is being used to encode missing values.
To fix the problem, we must provide pd.read_csv() with an argument called na_values.
Now, each instance of ? in the file is replaced with the
value np.nan, which means not a number:
Auto = pd.read_csv('Auto.data',
na_values=['?'],
delim_whitespace=True)
Auto['horsepower'].sum()
40952.0
The Auto.shape attribute tells us that the data has 397
observations, or rows, and nine variables, or columns.
Auto.shape
(397, 9)
There are
various ways to deal with missing data.
In this case, since only five of the rows contain missing
observations, we choose to use the Auto.dropna() method to simply remove these rows.
Auto_new = Auto.dropna()
Auto_new.shape
(392, 9)
Basics of Selecting Rows and Columns#
We can use Auto.columns to check the variable names.
Auto = Auto_new # overwrite the previous value
Auto.columns
Index(['mpg', 'cylinders', 'displacement', 'horsepower', 'weight',
'acceleration', 'year', 'origin', 'name'],
dtype='object')
Accessing the rows and columns of a data frame is similar, but not identical, to accessing the rows and columns of an array.
Recall that the first argument to the [] method
is always applied to the rows of the array.
Similarly,
passing in a slice to the [] method creates a data frame whose rows are determined by the slice:
Auto[:3]
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | name | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 18.0 | 8 | 307.0 | 130.0 | 3504.0 | 12.0 | 70 | 1 | chevrolet chevelle malibu |
| 1 | 15.0 | 8 | 350.0 | 165.0 | 3693.0 | 11.5 | 70 | 1 | buick skylark 320 |
| 2 | 18.0 | 8 | 318.0 | 150.0 | 3436.0 | 11.0 | 70 | 1 | plymouth satellite |
Similarly, an array of Booleans can be used to subset the rows:
idx_80 = Auto['year'] > 80
Auto[idx_80]
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | name | |
|---|---|---|---|---|---|---|---|---|---|
| 338 | 27.2 | 4 | 135.0 | 84.0 | 2490.0 | 15.7 | 81 | 1 | plymouth reliant |
| 339 | 26.6 | 4 | 151.0 | 84.0 | 2635.0 | 16.4 | 81 | 1 | buick skylark |
| 340 | 25.8 | 4 | 156.0 | 92.0 | 2620.0 | 14.4 | 81 | 1 | dodge aries wagon (sw) |
| 341 | 23.5 | 6 | 173.0 | 110.0 | 2725.0 | 12.6 | 81 | 1 | chevrolet citation |
| 342 | 30.0 | 4 | 135.0 | 84.0 | 2385.0 | 12.9 | 81 | 1 | plymouth reliant |
| 343 | 39.1 | 4 | 79.0 | 58.0 | 1755.0 | 16.9 | 81 | 3 | toyota starlet |
| 344 | 39.0 | 4 | 86.0 | 64.0 | 1875.0 | 16.4 | 81 | 1 | plymouth champ |
| 345 | 35.1 | 4 | 81.0 | 60.0 | 1760.0 | 16.1 | 81 | 3 | honda civic 1300 |
| 346 | 32.3 | 4 | 97.0 | 67.0 | 2065.0 | 17.8 | 81 | 3 | subaru |
| 347 | 37.0 | 4 | 85.0 | 65.0 | 1975.0 | 19.4 | 81 | 3 | datsun 210 mpg |
| 348 | 37.7 | 4 | 89.0 | 62.0 | 2050.0 | 17.3 | 81 | 3 | toyota tercel |
| 349 | 34.1 | 4 | 91.0 | 68.0 | 1985.0 | 16.0 | 81 | 3 | mazda glc 4 |
| 350 | 34.7 | 4 | 105.0 | 63.0 | 2215.0 | 14.9 | 81 | 1 | plymouth horizon 4 |
| 351 | 34.4 | 4 | 98.0 | 65.0 | 2045.0 | 16.2 | 81 | 1 | ford escort 4w |
| 352 | 29.9 | 4 | 98.0 | 65.0 | 2380.0 | 20.7 | 81 | 1 | ford escort 2h |
| 353 | 33.0 | 4 | 105.0 | 74.0 | 2190.0 | 14.2 | 81 | 2 | volkswagen jetta |
| 355 | 33.7 | 4 | 107.0 | 75.0 | 2210.0 | 14.4 | 81 | 3 | honda prelude |
| 356 | 32.4 | 4 | 108.0 | 75.0 | 2350.0 | 16.8 | 81 | 3 | toyota corolla |
| 357 | 32.9 | 4 | 119.0 | 100.0 | 2615.0 | 14.8 | 81 | 3 | datsun 200sx |
| 358 | 31.6 | 4 | 120.0 | 74.0 | 2635.0 | 18.3 | 81 | 3 | mazda 626 |
| 359 | 28.1 | 4 | 141.0 | 80.0 | 3230.0 | 20.4 | 81 | 2 | peugeot 505s turbo diesel |
| 360 | 30.7 | 6 | 145.0 | 76.0 | 3160.0 | 19.6 | 81 | 2 | volvo diesel |
| 361 | 25.4 | 6 | 168.0 | 116.0 | 2900.0 | 12.6 | 81 | 3 | toyota cressida |
| 362 | 24.2 | 6 | 146.0 | 120.0 | 2930.0 | 13.8 | 81 | 3 | datsun 810 maxima |
| 363 | 22.4 | 6 | 231.0 | 110.0 | 3415.0 | 15.8 | 81 | 1 | buick century |
| 364 | 26.6 | 8 | 350.0 | 105.0 | 3725.0 | 19.0 | 81 | 1 | oldsmobile cutlass ls |
| 365 | 20.2 | 6 | 200.0 | 88.0 | 3060.0 | 17.1 | 81 | 1 | ford granada gl |
| 366 | 17.6 | 6 | 225.0 | 85.0 | 3465.0 | 16.6 | 81 | 1 | chrysler lebaron salon |
| 367 | 28.0 | 4 | 112.0 | 88.0 | 2605.0 | 19.6 | 82 | 1 | chevrolet cavalier |
| 368 | 27.0 | 4 | 112.0 | 88.0 | 2640.0 | 18.6 | 82 | 1 | chevrolet cavalier wagon |
| 369 | 34.0 | 4 | 112.0 | 88.0 | 2395.0 | 18.0 | 82 | 1 | chevrolet cavalier 2-door |
| 370 | 31.0 | 4 | 112.0 | 85.0 | 2575.0 | 16.2 | 82 | 1 | pontiac j2000 se hatchback |
| 371 | 29.0 | 4 | 135.0 | 84.0 | 2525.0 | 16.0 | 82 | 1 | dodge aries se |
| 372 | 27.0 | 4 | 151.0 | 90.0 | 2735.0 | 18.0 | 82 | 1 | pontiac phoenix |
| 373 | 24.0 | 4 | 140.0 | 92.0 | 2865.0 | 16.4 | 82 | 1 | ford fairmont futura |
| 374 | 36.0 | 4 | 105.0 | 74.0 | 1980.0 | 15.3 | 82 | 2 | volkswagen rabbit l |
| 375 | 37.0 | 4 | 91.0 | 68.0 | 2025.0 | 18.2 | 82 | 3 | mazda glc custom l |
| 376 | 31.0 | 4 | 91.0 | 68.0 | 1970.0 | 17.6 | 82 | 3 | mazda glc custom |
| 377 | 38.0 | 4 | 105.0 | 63.0 | 2125.0 | 14.7 | 82 | 1 | plymouth horizon miser |
| 378 | 36.0 | 4 | 98.0 | 70.0 | 2125.0 | 17.3 | 82 | 1 | mercury lynx l |
| 379 | 36.0 | 4 | 120.0 | 88.0 | 2160.0 | 14.5 | 82 | 3 | nissan stanza xe |
| 380 | 36.0 | 4 | 107.0 | 75.0 | 2205.0 | 14.5 | 82 | 3 | honda accord |
| 381 | 34.0 | 4 | 108.0 | 70.0 | 2245.0 | 16.9 | 82 | 3 | toyota corolla |
| 382 | 38.0 | 4 | 91.0 | 67.0 | 1965.0 | 15.0 | 82 | 3 | honda civic |
| 383 | 32.0 | 4 | 91.0 | 67.0 | 1965.0 | 15.7 | 82 | 3 | honda civic (auto) |
| 384 | 38.0 | 4 | 91.0 | 67.0 | 1995.0 | 16.2 | 82 | 3 | datsun 310 gx |
| 385 | 25.0 | 6 | 181.0 | 110.0 | 2945.0 | 16.4 | 82 | 1 | buick century limited |
| 386 | 38.0 | 6 | 262.0 | 85.0 | 3015.0 | 17.0 | 82 | 1 | oldsmobile cutlass ciera (diesel) |
| 387 | 26.0 | 4 | 156.0 | 92.0 | 2585.0 | 14.5 | 82 | 1 | chrysler lebaron medallion |
| 388 | 22.0 | 6 | 232.0 | 112.0 | 2835.0 | 14.7 | 82 | 1 | ford granada l |
| 389 | 32.0 | 4 | 144.0 | 96.0 | 2665.0 | 13.9 | 82 | 3 | toyota celica gt |
| 390 | 36.0 | 4 | 135.0 | 84.0 | 2370.0 | 13.0 | 82 | 1 | dodge charger 2.2 |
| 391 | 27.0 | 4 | 151.0 | 90.0 | 2950.0 | 17.3 | 82 | 1 | chevrolet camaro |
| 392 | 27.0 | 4 | 140.0 | 86.0 | 2790.0 | 15.6 | 82 | 1 | ford mustang gl |
| 393 | 44.0 | 4 | 97.0 | 52.0 | 2130.0 | 24.6 | 82 | 2 | vw pickup |
| 394 | 32.0 | 4 | 135.0 | 84.0 | 2295.0 | 11.6 | 82 | 1 | dodge rampage |
| 395 | 28.0 | 4 | 120.0 | 79.0 | 2625.0 | 18.6 | 82 | 1 | ford ranger |
| 396 | 31.0 | 4 | 119.0 | 82.0 | 2720.0 | 19.4 | 82 | 1 | chevy s-10 |
However, if we pass in a list of strings to the [] method, then we obtain a data frame containing the corresponding set of columns.
Auto[['mpg', 'horsepower']]
| mpg | horsepower | |
|---|---|---|
| 0 | 18.0 | 130.0 |
| 1 | 15.0 | 165.0 |
| 2 | 18.0 | 150.0 |
| 3 | 16.0 | 150.0 |
| 4 | 17.0 | 140.0 |
| ... | ... | ... |
| 392 | 27.0 | 86.0 |
| 393 | 44.0 | 52.0 |
| 394 | 32.0 | 84.0 |
| 395 | 28.0 | 79.0 |
| 396 | 31.0 | 82.0 |
392 rows × 2 columns
Since we did not specify an index column when we loaded our data frame, the rows are labeled using integers 0 to 396.
Auto.index
Int64Index([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
...
387, 388, 389, 390, 391, 392, 393, 394, 395, 396],
dtype='int64', length=392)
We can use the
set_index() method to re-name the rows using the contents of Auto['name'].
Auto_re = Auto.set_index('name')
Auto_re
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | |
|---|---|---|---|---|---|---|---|---|
| name | ||||||||
| chevrolet chevelle malibu | 18.0 | 8 | 307.0 | 130.0 | 3504.0 | 12.0 | 70 | 1 |
| buick skylark 320 | 15.0 | 8 | 350.0 | 165.0 | 3693.0 | 11.5 | 70 | 1 |
| plymouth satellite | 18.0 | 8 | 318.0 | 150.0 | 3436.0 | 11.0 | 70 | 1 |
| amc rebel sst | 16.0 | 8 | 304.0 | 150.0 | 3433.0 | 12.0 | 70 | 1 |
| ford torino | 17.0 | 8 | 302.0 | 140.0 | 3449.0 | 10.5 | 70 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| ford mustang gl | 27.0 | 4 | 140.0 | 86.0 | 2790.0 | 15.6 | 82 | 1 |
| vw pickup | 44.0 | 4 | 97.0 | 52.0 | 2130.0 | 24.6 | 82 | 2 |
| dodge rampage | 32.0 | 4 | 135.0 | 84.0 | 2295.0 | 11.6 | 82 | 1 |
| ford ranger | 28.0 | 4 | 120.0 | 79.0 | 2625.0 | 18.6 | 82 | 1 |
| chevy s-10 | 31.0 | 4 | 119.0 | 82.0 | 2720.0 | 19.4 | 82 | 1 |
392 rows × 8 columns
Auto_re.columns
Index(['mpg', 'cylinders', 'displacement', 'horsepower', 'weight',
'acceleration', 'year', 'origin'],
dtype='object')
We see that the column 'name' is no longer there.
Now that the index has been set to name, we can access rows of the data
frame by name using the {loc[]} method of
Auto:
rows = ['amc rebel sst', 'ford torino']
Auto_re.loc[rows]
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | |
|---|---|---|---|---|---|---|---|---|
| name | ||||||||
| amc rebel sst | 16.0 | 8 | 304.0 | 150.0 | 3433.0 | 12.0 | 70 | 1 |
| ford torino | 17.0 | 8 | 302.0 | 140.0 | 3449.0 | 10.5 | 70 | 1 |
As an alternative to using the index name, we could retrieve the 4th and 5th rows of Auto using the {iloc[]} method:
Auto_re.iloc[[3,4]]
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | |
|---|---|---|---|---|---|---|---|---|
| name | ||||||||
| amc rebel sst | 16.0 | 8 | 304.0 | 150.0 | 3433.0 | 12.0 | 70 | 1 |
| ford torino | 17.0 | 8 | 302.0 | 140.0 | 3449.0 | 10.5 | 70 | 1 |
We can also use it to retrieve the 1st, 3rd and and 4th columns of Auto_re:
Auto_re.iloc[:,[0,2,3]]
| mpg | displacement | horsepower | |
|---|---|---|---|
| name | |||
| chevrolet chevelle malibu | 18.0 | 307.0 | 130.0 |
| buick skylark 320 | 15.0 | 350.0 | 165.0 |
| plymouth satellite | 18.0 | 318.0 | 150.0 |
| amc rebel sst | 16.0 | 304.0 | 150.0 |
| ford torino | 17.0 | 302.0 | 140.0 |
| ... | ... | ... | ... |
| ford mustang gl | 27.0 | 140.0 | 86.0 |
| vw pickup | 44.0 | 97.0 | 52.0 |
| dodge rampage | 32.0 | 135.0 | 84.0 |
| ford ranger | 28.0 | 120.0 | 79.0 |
| chevy s-10 | 31.0 | 119.0 | 82.0 |
392 rows × 3 columns
We can extract the 4th and 5th rows, as well as the 1st, 3rd and 4th columns, using
a single call to iloc[]:
Auto_re.iloc[[3,4],[0,2,3]]
| mpg | displacement | horsepower | |
|---|---|---|---|
| name | |||
| amc rebel sst | 16.0 | 304.0 | 150.0 |
| ford torino | 17.0 | 302.0 | 140.0 |
Index entries need not be unique: there are several cars in the data frame named ford galaxie 500.
Auto_re.loc['ford galaxie 500', ['mpg', 'origin']]
| mpg | origin | |
|---|---|---|
| name | ||
| ford galaxie 500 | 15.0 | 1 |
| ford galaxie 500 | 14.0 | 1 |
| ford galaxie 500 | 14.0 | 1 |
More on Selecting Rows and Columns#
Suppose now that we want to create a data frame consisting of the weight and origin of the subset of cars with
year greater than 80 — i.e. those built after 1980.
To do this, we first create a Boolean array that indexes the rows.
The loc[] method allows for Boolean entries as well as strings:
idx_80 = Auto_re['year'] > 80
Auto_re.loc[idx_80, ['weight', 'origin']]
| weight | origin | |
|---|---|---|
| name | ||
| plymouth reliant | 2490.0 | 1 |
| buick skylark | 2635.0 | 1 |
| dodge aries wagon (sw) | 2620.0 | 1 |
| chevrolet citation | 2725.0 | 1 |
| plymouth reliant | 2385.0 | 1 |
| toyota starlet | 1755.0 | 3 |
| plymouth champ | 1875.0 | 1 |
| honda civic 1300 | 1760.0 | 3 |
| subaru | 2065.0 | 3 |
| datsun 210 mpg | 1975.0 | 3 |
| toyota tercel | 2050.0 | 3 |
| mazda glc 4 | 1985.0 | 3 |
| plymouth horizon 4 | 2215.0 | 1 |
| ford escort 4w | 2045.0 | 1 |
| ford escort 2h | 2380.0 | 1 |
| volkswagen jetta | 2190.0 | 2 |
| honda prelude | 2210.0 | 3 |
| toyota corolla | 2350.0 | 3 |
| datsun 200sx | 2615.0 | 3 |
| mazda 626 | 2635.0 | 3 |
| peugeot 505s turbo diesel | 3230.0 | 2 |
| volvo diesel | 3160.0 | 2 |
| toyota cressida | 2900.0 | 3 |
| datsun 810 maxima | 2930.0 | 3 |
| buick century | 3415.0 | 1 |
| oldsmobile cutlass ls | 3725.0 | 1 |
| ford granada gl | 3060.0 | 1 |
| chrysler lebaron salon | 3465.0 | 1 |
| chevrolet cavalier | 2605.0 | 1 |
| chevrolet cavalier wagon | 2640.0 | 1 |
| chevrolet cavalier 2-door | 2395.0 | 1 |
| pontiac j2000 se hatchback | 2575.0 | 1 |
| dodge aries se | 2525.0 | 1 |
| pontiac phoenix | 2735.0 | 1 |
| ford fairmont futura | 2865.0 | 1 |
| volkswagen rabbit l | 1980.0 | 2 |
| mazda glc custom l | 2025.0 | 3 |
| mazda glc custom | 1970.0 | 3 |
| plymouth horizon miser | 2125.0 | 1 |
| mercury lynx l | 2125.0 | 1 |
| nissan stanza xe | 2160.0 | 3 |
| honda accord | 2205.0 | 3 |
| toyota corolla | 2245.0 | 3 |
| honda civic | 1965.0 | 3 |
| honda civic (auto) | 1965.0 | 3 |
| datsun 310 gx | 1995.0 | 3 |
| buick century limited | 2945.0 | 1 |
| oldsmobile cutlass ciera (diesel) | 3015.0 | 1 |
| chrysler lebaron medallion | 2585.0 | 1 |
| ford granada l | 2835.0 | 1 |
| toyota celica gt | 2665.0 | 3 |
| dodge charger 2.2 | 2370.0 | 1 |
| chevrolet camaro | 2950.0 | 1 |
| ford mustang gl | 2790.0 | 1 |
| vw pickup | 2130.0 | 2 |
| dodge rampage | 2295.0 | 1 |
| ford ranger | 2625.0 | 1 |
| chevy s-10 | 2720.0 | 1 |
To do this more concisely, we can use an anonymous function called a lambda:
Auto_re.loc[lambda df: df['year'] > 80, ['weight', 'origin']]
| weight | origin | |
|---|---|---|
| name | ||
| plymouth reliant | 2490.0 | 1 |
| buick skylark | 2635.0 | 1 |
| dodge aries wagon (sw) | 2620.0 | 1 |
| chevrolet citation | 2725.0 | 1 |
| plymouth reliant | 2385.0 | 1 |
| toyota starlet | 1755.0 | 3 |
| plymouth champ | 1875.0 | 1 |
| honda civic 1300 | 1760.0 | 3 |
| subaru | 2065.0 | 3 |
| datsun 210 mpg | 1975.0 | 3 |
| toyota tercel | 2050.0 | 3 |
| mazda glc 4 | 1985.0 | 3 |
| plymouth horizon 4 | 2215.0 | 1 |
| ford escort 4w | 2045.0 | 1 |
| ford escort 2h | 2380.0 | 1 |
| volkswagen jetta | 2190.0 | 2 |
| honda prelude | 2210.0 | 3 |
| toyota corolla | 2350.0 | 3 |
| datsun 200sx | 2615.0 | 3 |
| mazda 626 | 2635.0 | 3 |
| peugeot 505s turbo diesel | 3230.0 | 2 |
| volvo diesel | 3160.0 | 2 |
| toyota cressida | 2900.0 | 3 |
| datsun 810 maxima | 2930.0 | 3 |
| buick century | 3415.0 | 1 |
| oldsmobile cutlass ls | 3725.0 | 1 |
| ford granada gl | 3060.0 | 1 |
| chrysler lebaron salon | 3465.0 | 1 |
| chevrolet cavalier | 2605.0 | 1 |
| chevrolet cavalier wagon | 2640.0 | 1 |
| chevrolet cavalier 2-door | 2395.0 | 1 |
| pontiac j2000 se hatchback | 2575.0 | 1 |
| dodge aries se | 2525.0 | 1 |
| pontiac phoenix | 2735.0 | 1 |
| ford fairmont futura | 2865.0 | 1 |
| volkswagen rabbit l | 1980.0 | 2 |
| mazda glc custom l | 2025.0 | 3 |
| mazda glc custom | 1970.0 | 3 |
| plymouth horizon miser | 2125.0 | 1 |
| mercury lynx l | 2125.0 | 1 |
| nissan stanza xe | 2160.0 | 3 |
| honda accord | 2205.0 | 3 |
| toyota corolla | 2245.0 | 3 |
| honda civic | 1965.0 | 3 |
| honda civic (auto) | 1965.0 | 3 |
| datsun 310 gx | 1995.0 | 3 |
| buick century limited | 2945.0 | 1 |
| oldsmobile cutlass ciera (diesel) | 3015.0 | 1 |
| chrysler lebaron medallion | 2585.0 | 1 |
| ford granada l | 2835.0 | 1 |
| toyota celica gt | 2665.0 | 3 |
| dodge charger 2.2 | 2370.0 | 1 |
| chevrolet camaro | 2950.0 | 1 |
| ford mustang gl | 2790.0 | 1 |
| vw pickup | 2130.0 | 2 |
| dodge rampage | 2295.0 | 1 |
| ford ranger | 2625.0 | 1 |
| chevy s-10 | 2720.0 | 1 |
The lambda call creates a function that takes a single
argument, here df, and returns df['year']>80.
Since it is created inside the loc[] method for the
dataframe Auto_re, that dataframe will be the argument supplied.
As another example of using a lambda, suppose that
we want all cars built after 1980 that achieve greater than 30 miles per gallon:
Auto_re.loc[lambda df: (df['year'] > 80) & (df['mpg'] > 30),
['weight', 'origin']
]
| weight | origin | |
|---|---|---|
| name | ||
| toyota starlet | 1755.0 | 3 |
| plymouth champ | 1875.0 | 1 |
| honda civic 1300 | 1760.0 | 3 |
| subaru | 2065.0 | 3 |
| datsun 210 mpg | 1975.0 | 3 |
| toyota tercel | 2050.0 | 3 |
| mazda glc 4 | 1985.0 | 3 |
| plymouth horizon 4 | 2215.0 | 1 |
| ford escort 4w | 2045.0 | 1 |
| volkswagen jetta | 2190.0 | 2 |
| honda prelude | 2210.0 | 3 |
| toyota corolla | 2350.0 | 3 |
| datsun 200sx | 2615.0 | 3 |
| mazda 626 | 2635.0 | 3 |
| volvo diesel | 3160.0 | 2 |
| chevrolet cavalier 2-door | 2395.0 | 1 |
| pontiac j2000 se hatchback | 2575.0 | 1 |
| volkswagen rabbit l | 1980.0 | 2 |
| mazda glc custom l | 2025.0 | 3 |
| mazda glc custom | 1970.0 | 3 |
| plymouth horizon miser | 2125.0 | 1 |
| mercury lynx l | 2125.0 | 1 |
| nissan stanza xe | 2160.0 | 3 |
| honda accord | 2205.0 | 3 |
| toyota corolla | 2245.0 | 3 |
| honda civic | 1965.0 | 3 |
| honda civic (auto) | 1965.0 | 3 |
| datsun 310 gx | 1995.0 | 3 |
| oldsmobile cutlass ciera (diesel) | 3015.0 | 1 |
| toyota celica gt | 2665.0 | 3 |
| dodge charger 2.2 | 2370.0 | 1 |
| vw pickup | 2130.0 | 2 |
| dodge rampage | 2295.0 | 1 |
| chevy s-10 | 2720.0 | 1 |
The symbol & computes an element-wise and operation.
As another example, suppose that we want to retrieve all Ford and Datsun
cars with displacement less than 300. We check whether each name entry contains either the string ford or datsun using the str.contains() method of the index attribute of
of the dataframe:
Auto_re.loc[lambda df: (df['displacement'] < 300)
& (df.index.str.contains('ford')
| df.index.str.contains('datsun')),
['weight', 'origin']
]
| weight | origin | |
|---|---|---|
| name | ||
| ford maverick | 2587.0 | 1 |
| datsun pl510 | 2130.0 | 3 |
| datsun pl510 | 2130.0 | 3 |
| ford torino 500 | 3302.0 | 1 |
| ford mustang | 3139.0 | 1 |
| datsun 1200 | 1613.0 | 3 |
| ford pinto runabout | 2226.0 | 1 |
| ford pinto (sw) | 2395.0 | 1 |
| datsun 510 (sw) | 2288.0 | 3 |
| ford maverick | 3021.0 | 1 |
| datsun 610 | 2379.0 | 3 |
| ford pinto | 2310.0 | 1 |
| datsun b210 | 1950.0 | 3 |
| ford pinto | 2451.0 | 1 |
| datsun 710 | 2003.0 | 3 |
| ford maverick | 3158.0 | 1 |
| ford pinto | 2639.0 | 1 |
| datsun 710 | 2545.0 | 3 |
| ford pinto | 2984.0 | 1 |
| ford maverick | 3012.0 | 1 |
| ford granada ghia | 3574.0 | 1 |
| datsun b-210 | 1990.0 | 3 |
| ford pinto | 2565.0 | 1 |
| datsun f-10 hatchback | 1945.0 | 3 |
| ford granada | 3525.0 | 1 |
| ford mustang ii 2+2 | 2755.0 | 1 |
| datsun 810 | 2815.0 | 3 |
| ford fiesta | 1800.0 | 1 |
| datsun b210 gx | 2070.0 | 3 |
| ford fairmont (auto) | 2965.0 | 1 |
| ford fairmont (man) | 2720.0 | 1 |
| datsun 510 | 2300.0 | 3 |
| datsun 200-sx | 2405.0 | 3 |
| ford fairmont 4 | 2890.0 | 1 |
| datsun 210 | 2020.0 | 3 |
| datsun 310 | 2019.0 | 3 |
| ford fairmont | 2870.0 | 1 |
| datsun 510 hatchback | 2434.0 | 3 |
| datsun 210 | 2110.0 | 3 |
| datsun 280-zx | 2910.0 | 3 |
| datsun 210 mpg | 1975.0 | 3 |
| ford escort 4w | 2045.0 | 1 |
| ford escort 2h | 2380.0 | 1 |
| datsun 200sx | 2615.0 | 3 |
| datsun 810 maxima | 2930.0 | 3 |
| ford granada gl | 3060.0 | 1 |
| ford fairmont futura | 2865.0 | 1 |
| datsun 310 gx | 1995.0 | 3 |
| ford granada l | 2835.0 | 1 |
| ford mustang gl | 2790.0 | 1 |
| ford ranger | 2625.0 | 1 |
Here, the symbol | computes an element-wise or operation.
In summary, a powerful set of operations is available to index the rows and columns of data frames. For integer based queries, use the iloc[] method. For string and Boolean
selections, use the loc[] method. For functional queries that filter rows, use the loc[] method
with a function (typically a lambda) in the rows argument.
For Loops#
A for loop is a standard tool in many languages that
repeatedly evaluates some chunk of code while
varying different values inside the code.
For example, suppose we loop over elements of a list and compute their sum.
total = 0
for value in [3,2,19]:
total += value
print('Total is: {0}'.format(total))
Total is: 24
The indented code beneath the line with the for statement is run
for each value in the sequence
specified in the for statement. The loop ends either
when the cell ends or when code is indented at the same level
as the original for statement.
We see that the final line above which prints the total is executed
only once after the for loop has terminated. Loops
can be nested by additional indentation.
total = 0
for value in [2,3,19]:
for weight in [3, 2, 1]:
total += value * weight
print('Total is: {0}'.format(total))
Total is: 144
Above, we summed over each combination of value and weight.
We also took advantage of the increment notation
in Python: the expression a += b is equivalent
to a = a + b. Besides
being a convenient notation, this can save time in computationally
heavy tasks in which the intermediate value of a+b need not
be explicitly created.
Perhaps a more
common task would be to sum over (value, weight) pairs. For instance,
to compute the average value of a random variable that takes on
possible values 2, 3 or 19 with probability 0.2, 0.3, 0.5 respectively
we would compute the weighted sum. Tasks such as this
can often be accomplished using the zip() function that
loops over a sequence of tuples.
total = 0
for value, weight in zip([2,3,19],
[0.2,0.3,0.5]):
total += weight * value
print('Weighted average is: {0}'.format(total))
Weighted average is: 10.8
String Formatting#
In the code chunk above we also printed a string
displaying the total. However, the object total
is an integer and not a string.
Inserting the value of something into
a string is a common task, made
simple using
some of the powerful string formatting
tools in Python.
Many data cleaning tasks involve
manipulating and programmatically
producing strings.
For example we may want to loop over the columns of a data frame and
print the percent missing in each column.
Let’s create a data frame D with columns in which 20% of the entries are missing i.e. set
to np.nan. We’ll create the
values in D from a normal distribution with mean 0 and variance 1 using rng.standard_normal()
and then overwrite some random entries using rng.choice().
rng = np.random.default_rng(1)
A = rng.standard_normal((127, 5))
M = rng.choice([0, np.nan], p=[0.8,0.2], size=A.shape)
A += M
D = pd.DataFrame(A, columns=['food',
'bar',
'pickle',
'snack',
'popcorn'])
D[:3]
| food | bar | pickle | snack | popcorn | |
|---|---|---|---|---|---|
| 0 | 0.345584 | 0.821618 | 0.330437 | -1.303157 | NaN |
| 1 | NaN | -0.536953 | 0.581118 | 0.364572 | 0.294132 |
| 2 | NaN | 0.546713 | NaN | -0.162910 | -0.482119 |
for col in D.columns:
template = 'Column "{0}" has {1:.2%} missing values'
print(template.format(col,
np.isnan(D[col]).mean()))
Column "food" has 16.54% missing values
Column "bar" has 25.98% missing values
Column "pickle" has 29.13% missing values
Column "snack" has 21.26% missing values
Column "popcorn" has 22.83% missing values
We see that the template.format() method expects two arguments {0}
and {1:.2%}, and the latter includes some formatting
information. In particular, it specifies that the second argument should be expressed as a percent with two decimal digits.
The reference docs.python.org/3/library/string.html includes many helpful and more complex examples.
Additional Graphical and Numerical Summaries#
We can use the ax.plot() or ax.scatter() functions to display the quantitative variables. However, simply typing the variable names will produce an error message,
because Python does not know to look in the Auto data set for those variables.
fig, ax = subplots(figsize=(8, 8))
ax.plot(horsepower, mpg, 'o');
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[102], line 2
1 fig, ax = subplots(figsize=(8, 8))
----> 2 ax.plot(horsepower, mpg, 'o');
NameError: name 'horsepower' is not defined

We can address this by accessing the columns directly:
fig, ax = subplots(figsize=(8, 8))
ax.plot(Auto['horsepower'], Auto['mpg'], 'o');
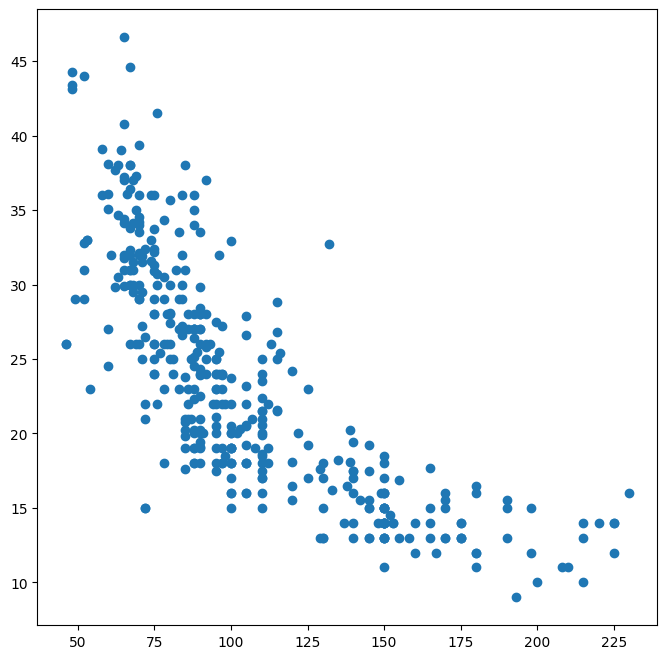
Alternatively, we can use the plot() method with the call Auto.plot().
Using this method,
the variables can be accessed by name.
The plot methods of a data frame return a familiar object:
an axes. We can use it to update the plot as we did previously:
ax = Auto.plot.scatter('horsepower', 'mpg');
ax.set_title('Horsepower vs. MPG')
Text(0.5, 1.0, 'Horsepower vs. MPG')
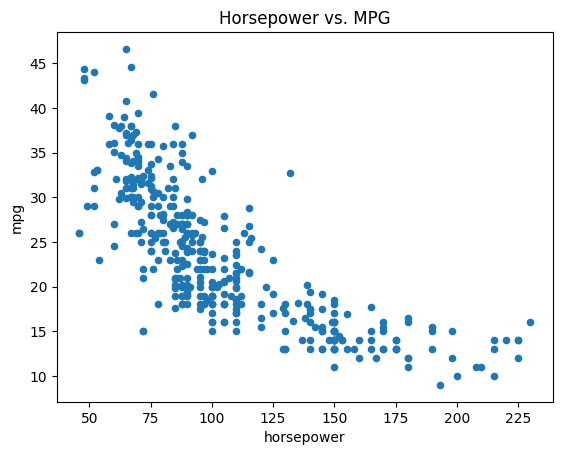
If we want to save
the figure that contains a given axes, we can find the relevant figure
by accessing the figure attribute:
fig = ax.figure
fig.savefig('horsepower_mpg.png');
We can further instruct the data frame to plot to a particular axes object. In this
case the corresponding plot() method will return the
modified axes we passed in as an argument. Note that
when we request a one-dimensional grid of plots, the object axes is similarly
one-dimensional. We place our scatter plot in the middle plot of a row of three plots
within a figure.
fig, axes = subplots(ncols=3, figsize=(15, 5))
Auto.plot.scatter('horsepower', 'mpg', ax=axes[1]);
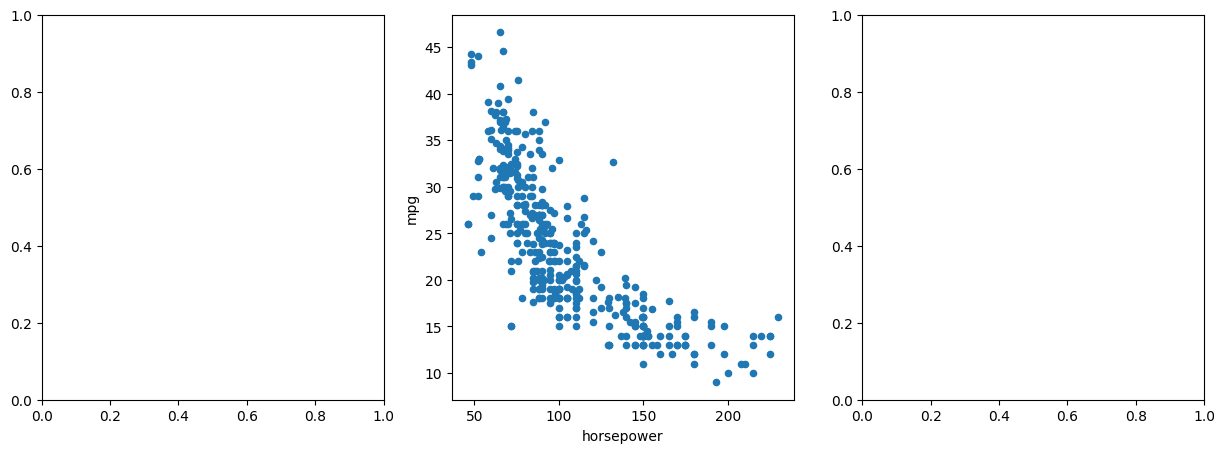
Note also that the columns of a data frame can be accessed as attributes: try typing in Auto.horsepower.
We now consider the cylinders variable. Typing in Auto.cylinders.dtype reveals that it is being treated as a quantitative variable.
However, since there is only a small number of possible values for this variable, we may wish to treat it as
qualitative. Below, we replace
the cylinders column with a categorical version of Auto.cylinders. The function pd.Series() owes its name to the fact that pandas is often used in time series applications.
Auto.cylinders = pd.Series(Auto.cylinders, dtype='category')
Auto.cylinders.dtype
CategoricalDtype(categories=[3, 4, 5, 6, 8], ordered=False)
Now that cylinders is qualitative, we can display it using
the boxplot() method.
fig, ax = subplots(figsize=(8, 8))
Auto.boxplot('mpg', by='cylinders', ax=ax);
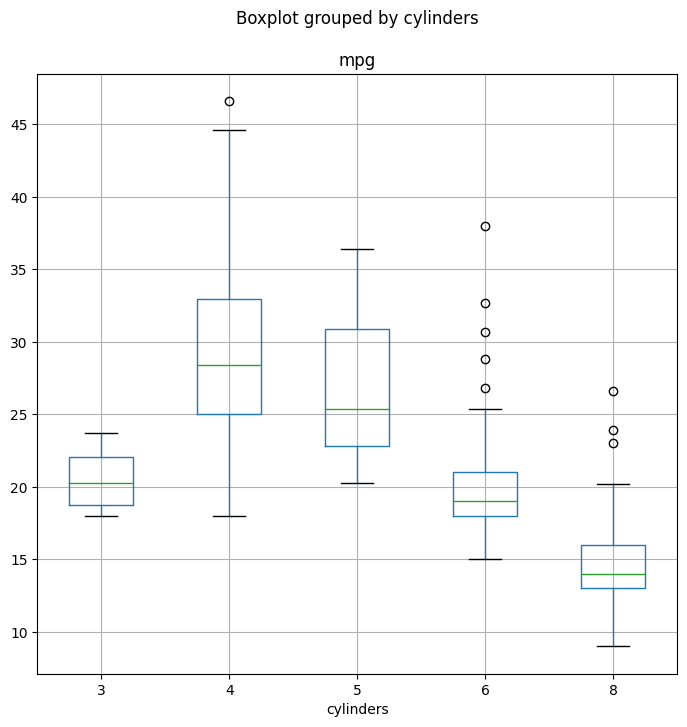
The hist() method can be used to plot a histogram.
fig, ax = subplots(figsize=(8, 8))
Auto.hist('mpg', ax=ax);
The color of the bars and the number of bins can be changed:
fig, ax = subplots(figsize=(8, 8))
Auto.hist('mpg', color='red', bins=12, ax=ax);
See Auto.hist? for more plotting
options.
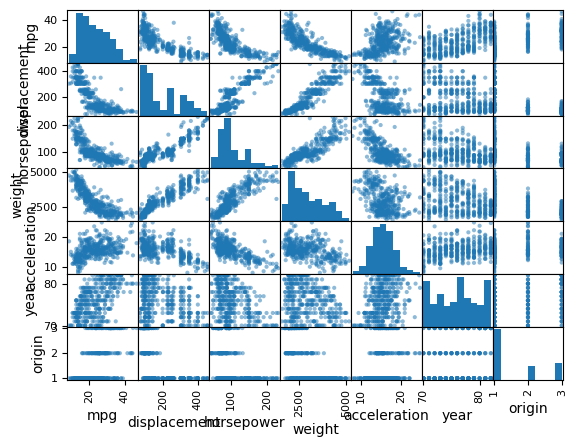
We can use the pd.plotting.scatter_matrix() function to create a scatterplot matrix to visualize all of the pairwise relationships between the columns in
a data frame.
pd.plotting.scatter_matrix(Auto);
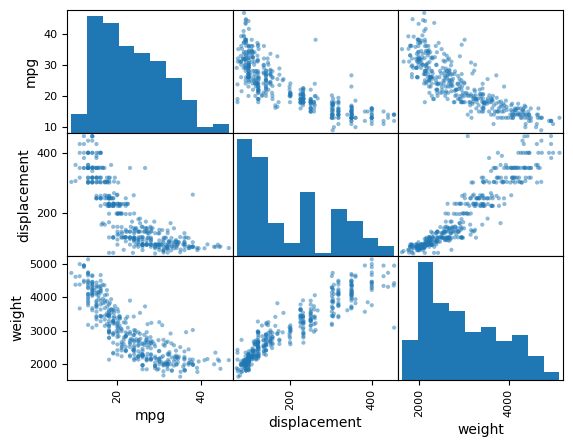
We can also produce scatterplots for a subset of the variables.
pd.plotting.scatter_matrix(Auto[['mpg',
'displacement',
'weight']]);
The describe() method produces a numerical summary of each column in a data frame.
Auto[['mpg', 'weight']].describe()
| mpg | weight | |
|---|---|---|
| count | 392.000000 | 392.000000 |
| mean | 23.445918 | 2977.584184 |
| std | 7.805007 | 849.402560 |
| min | 9.000000 | 1613.000000 |
| 25% | 17.000000 | 2225.250000 |
| 50% | 22.750000 | 2803.500000 |
| 75% | 29.000000 | 3614.750000 |
| max | 46.600000 | 5140.000000 |
We can also produce a summary of just a single column.
Auto['cylinders'].describe()
Auto['mpg'].describe()
count 392.000000
mean 23.445918
std 7.805007
min 9.000000
25% 17.000000
50% 22.750000
75% 29.000000
max 46.600000
Name: mpg, dtype: float64
To exit Jupyter, select File / Close and Halt.